Corso di laurea magistrale Interateneo in Fisica dei sistemi complessi

One of the most remarkable effects of highly viscous polymer solutions that has been recently observed in experiments is the development of an elastic turbulence regime in the limit of strong elasticity. The flow of polymer solution in this regime displays irregularities typical of turbulent flows even at low velocity and high viscosity (i.e., for vanishing Reynolds number). As a consequence of turbulent motion at small scales, elastic turbulence can reveal as an efficient technique for mixing in very low Reynolds flows (e.g., in microchannels). Despite its great technological interest, elastic turbulence is still only partially understood from a fundamental point of view.

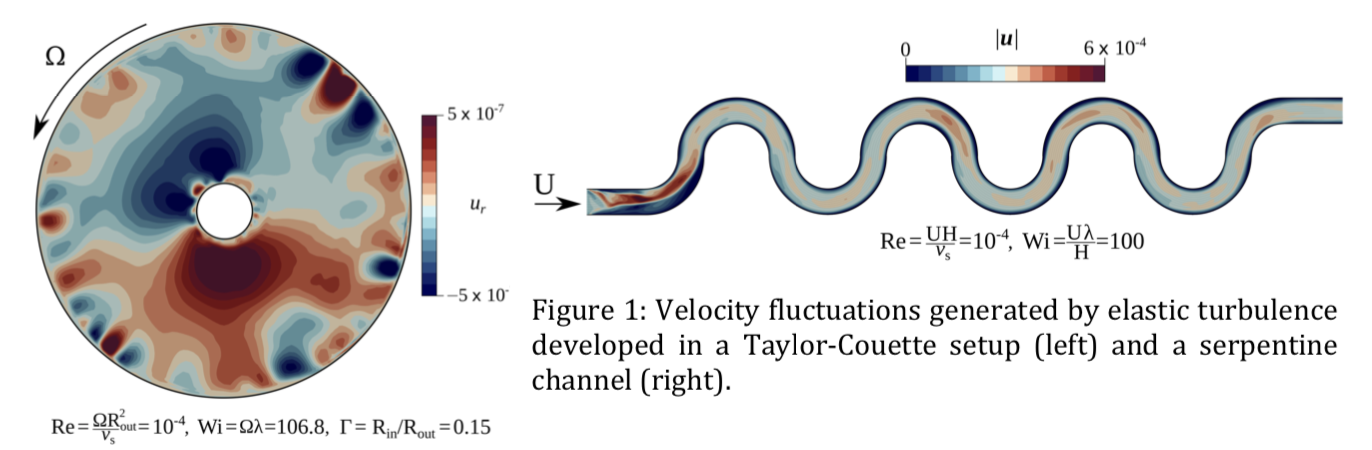
During this internship, we will build up on the results obtained in a previous internship that demonstrated the numerical reproducibility of elastic turbulence in a 2D Taylor-Couette (fig. 1, left) and a 2D serpentine channel (fig. 1, right). The analysis will focus on the Eulerian and Lagrangian mixing properties in these two setups, with the aim of relating them to the statistical behavior of velocity fluctuations as a function of the flow elasticity and the polymer concentration.